挑戦! word2vecで自然言語処理(Keras+TensorFlow使用):ディープラーニング習得、次の一歩(1/2 ページ)
自然言語のベクトル化手法の一つである「word2vec」を使って、単語間の関連性を表現してみよう。Keras(+TensorFlow)を使って実装する。
ご注意:本記事は、@IT/Deep Insider編集部(デジタルアドバンテージ社)が「deepinsider.jp」というサイトから、内容を改変することなく、そのまま「@IT」へと転載したものです。このため用字用語の統一ルールなどは@ITのそれとは一致しません。あらかじめご了承ください。
ディープラーニングと自然言語処理
画像認識や音声認識の分野では、すでに圧倒的ともいえる成果を誇っているのがディープラーニングである。猫画像識別のニュースに驚かされてからわずか数年のうちに、例えば「GAN(Generative Adversarial Network)」という技術が開発されていて、これを使うと、文字どおり何もないところから写真と見まがう画像を生成することができる。まさに、「十分に進歩した科学は魔法と区別がつかない」。
では、ディープラーニングのもう一方の有力分野である自然言語処理の状況はどうであろうか。こちらでは、「seq2seq(sequence to sequence)」という手法があって、それを応用したここ数年のWeb翻訳における非線形、不連続な精度の向上は、誰しもが体感するところである。
しかしながら、文章要約の分野では、学習データをどのようにして準備するのかという問題もあって、実用レベルへの到達はもう少し先のようである。録音データから議事録が自動で作成されるサービスがあれば大ヒット間違いなしと筆者などは思うわけであるが、それは差し当たり夢のままである。逆に言うと、これから開発されてくる技術がまだまだあるということであり、応用先の広さも相まって、自然言語処理分野では、近い将来さらに大きな波がやってくると筆者は考えている。
自然言語のベクトル化手法「word2vec」
自然言語をディープラーニングで扱う場合、何らかの方法で単語をベクトルデータに変換する必要がある。しゃれた言い方では、n次元実数空間への埋め込みであるが、要はn個の実数の組に対応させることである。とにかく、数字に変換しないと始まらない。
word2vecとは、このような自然言語のベクトル化手法の一つで、単語間の関連性を、対応するベクトル間演算(足し引き)で表現できるようにしよう、というものである。例えば、
king(の埋め込みベクトル) − man(の埋め込みベクトル) + woman(の埋め込みベクトル) = queen(の埋め込みベクトル)
が成り立つように埋め込みベクトルを決定する、ということである。結構途方もない話であるが、詳細は例えばMikolov他著の以下の論文を参照されたい。
また、上記の論文に関しては、筆者が作成したプレゼン資料がある。ご参考になれば幸いである。
本稿のゴール
word2vecのニューラルネットワーク(以下、ニューラルネット)を実際に構築して、日本語を対象としたベクトル表現を得る。日本語は形態素解析を用いて単語に分解し、単語単位にベクトル表現を得るようにする。
本稿では、Kerasを使って実装する。また、訓練データのボリュームは個人レベルでも取り扱いが容易な、数十万語程度の規模を想定している。この規模だと汎用的なベクトル表現の獲得は難しいが、算用数字と漢数字の関連付け(「一」 − 「1」 + 「2」 = 「二」)程度は実現できた。
なお、TensorFlowやKerasはインストール済みを前提に論を進める。
word2vecの特徴
自然言語のベクトル化手法にもいろいろあるが、一番単純なのが、one-hotベクトルへの変換である。語彙数がNであるとき、各単語に0からN-1までのインデックスiを振る。各単語に対し、i次元の値が1で、それ以外の値が0のベクトル(1つの次元だけが1で他が0のため、one-hotベクトルと呼ばれる)に対応させると、確かにN次元実数空間への埋め込みが実現できる。
しかしながら、この手法はニューラルネットの入力次元数が語彙数となるため、必然的に重み行列の要素数も巨大なものになる。これでは後々の訓練や予測がしんどいので、もっと入力次元を減らしたいところであるが、何とKerasには、その名も「Embedding」レイヤーというものが標準で用意されており、指定された次元への埋め込みベクトルを生成してくれる。例え語彙数が10000であっても、次元数を100と指定すれば、100次元の実数ベクトルが生成される。ベクトルの各要素はランダムに決定され、当然ながらone-hotベクトルではない。
word2vecはこのような、語彙数より少ない次元Embedding数のベクトル化手法である。その特徴は、先にも記したとおり、単語間の関連性をベクトル表現に反映しているところであるが、その手法には、CBOW(Continuous Bag-of-Words Model)とContinuous Skip-gram Model(以下、skip-gramと表記)の2種類がある。
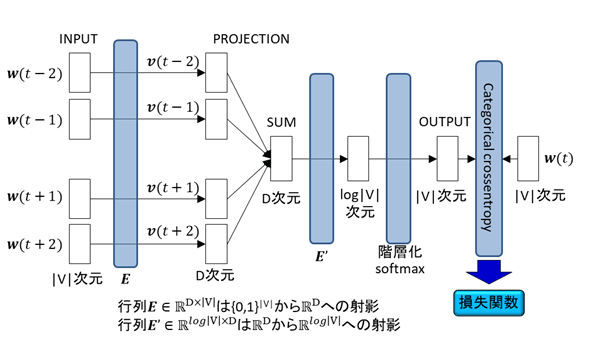
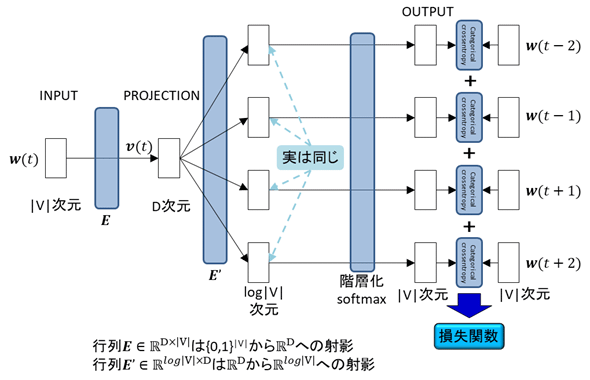
CBOWは、前後の単語からターゲットの単語を予測しようというものである。一方skip-gramはその逆に、特定の単語が与えられたときに、その前後の単語を当てようというものである。
以下にそれぞれのイメージを図示する。図においてVは語彙集合、|V|はその要素数すなわち語彙数、Dは埋め込みベクトルの次元である。また、wは各単語のone-hotベクトル表現、vはその埋め込みベクトル表現、Eはwからvへの変換行列、E'はvを後述する階層化softmax空間に射影する行列である。実装的には、EがKerasのEmbeddingレイヤー、E'がDenseレイヤーに相当する。畳み込みもLSTMも無く、MLP(Multi-Layer Perceptron、多層パーセプトロン)でもないシンプルなネットワーク構成が、word2vecの特徴である。
図の中にある、「階層化softmax」というのは、計算量削減の手法である。softmax算出時の次元数は、ラベルデータのone-hotベクトルとのcategorical_crossentropy(多クラスの交差エントロピー)計算を行う関係上、必ず語彙数になるが、訓練データである文章量が巨大になる(上述の論文では、億オーダの単語量の訓練データを使用している)と語彙数も膨大になり、常識的な時間内で計算が終わらなくなる。
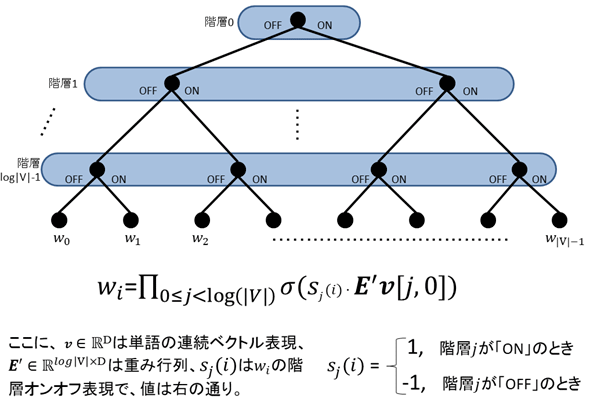
そこで階層化softmaxである。|V|次元出力ベクトルの|V|個のデータを2つに分け、それぞれをまた2つに分け、というように2分割を繰り返していくと、各要素を2分探索木に対応させることができ、その階層数は(だいたい)“log(|V|)”になる。各要素は各層の「オン/オフ」の組み合わせで一意に表現できるので、ニューラルネットのノードを各層に対応させると、出力ベクトル各要素の値は各層の活性化関数(2択なのでsigmoid)の積で表現できる。
すなわち、softmaxを用いずに出力ベクトルの確率分布表現を得ることができた。あとは普通にcategorical_crossentropyによる誤差評価を行うだけである。図3に階層化softmaxのイメージを示す。
なお、本稿は訓練データのボリュームを、個人が自宅PCで処理できる程度である数十万語程度と想定している。これくらいの量だと階層化softmaxを適用するまでもないので、以下、これを使用しない前提で論を進めていく。
訓練データの入手
ある程度のボリュームがある日本語テキストなら、何でもよい。筆者は青空文庫から、江戸川乱歩の著作を入手して使用した。後で形態素解析にかける関係上、現代仮名遣いの口語調の文書が良い。
形態素解析
形態素解析とは、簡単に言うと日本語の文章を単語に分解することである。今日では各種の形態素解析ソフトが利用可能になっているが、筆者は京大黒橋・河原研究室のJUMAN++を使用した。
以下にJUMAN++のURLを記す。ここからソフトウェアをダウンロードし、PCにインストールして対象文章を入力すると、分かち書きされた出力がカンマ区切りで得られるので、これをCSVファイルとして保存しておく。
JUMAN++の分かち書きは情報量が豊富だが、今回は分かち書きの結果(各行の先頭、つまりCSVに変換したときの一番左の列)のみ使用している。また、分割した単語に別の読み方がある場合、「@」で始まる行が出現するが、今回は不要なのでその行は削除しておく。
地の文の他に、ルビや、見出し指定などの記号が文書内に含まれている。筆者はそのまま学習に使用したが、ここは好みで取り除いてもよい。CSVファイルの加工には、筆者はExcelを使用した。
CSVファイルの取り込み
いよいよ実装である。ニューラルネット自体は前述のとおりEmbeddingとDenseだけなので、拍子抜けするくらい簡単である。コードの大部分は、元データの訓練データへの整形である。なお、参考情報として、筆者が実行したソースコードを以下に示す。これらをJupyter Notebook上で、コードブロック単位に実行した。
まず、各種import宣言である。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import csv
import pandas as pd
import random
import numpy.random as nr
import sys
import h5py
import math
from __future__ import print_function
from keras.layers.core import Activation
from keras.layers.core import Dense
from keras.layers.core import Flatten
from keras.models import Sequential
from keras.layers.embeddings import Embedding
from keras.callbacks import EarlyStopping
from keras.initializers import glorot_uniform
from keras.initializers import uniform
from keras.optimizers import RMSprop
from keras.utils import np_utils
次に、csv読み込み処理である。取り込みファイルが3つなのは、筆者が元テキストを3つに分けて形態素解析にかけたからで、時に意味はない。行方向(要は「下」方向)に結合して1つの行列にする。この時点で、行列の各要素はテキストである。
# 元データ
df1 = csv.reader(open('rampo_separate.csv', 'r'))
df2 = csv.reader(open('rampo_separate2.csv', 'r'))
df3 = csv.reader(open('rampo_separate3.csv', 'r'))
data1 = [ v for v in df1]
data2 = [ v for v in df2]
data3 = [ v for v in df3]
mat1 = np.array(data1)
mat2 = np.array(data2)
mat3 = np.array(data3)
mat = np.r_[mat1[:,0], mat2[:,0], mat3[:,0]]
print(mat.shape)
辞書データの作成
出現する単語に一意のインデックス番号を付与し、インデックス←→単語文字列の両引きが出来る辞書を作成する。
単語数が多いとニューラルネットの出力次元数が大きくなり、学習コストが高まる。そこで、出現頻度が低い単語(以下の事例では3回以下)は思い切って割り切り、十把ひとからげに「UNK」文字列に置き換える。これで、筆者の例では出力次元数が1/3以下になった。
ソースコード上では念のために置き換えた単語のリストを作成してあるが、その後の処理では使用していない。
words = sorted(list(set(mat)))
cnt = np.zeros(len(words))
print('total words:', len(words))
word_indices = dict((w, i) for i, w in enumerate(words)) # 単語をキーにインデックス検索
indices_word = dict((i, w) for i, w in enumerate(words)) # インデックスをキーに単語を検索
# 単語の出現数をカウント
for j in range (0, len(mat)):
cnt[word_indices[mat[j]]] += 1
# 出現頻度の少ない単語を「UNK」で置き換え
words_unk = [] # 未知語一覧
for k in range(0, len(words)):
if cnt[k] <= 3 :
words_unk.append(words[k])
words[k] = 'UNK'
print('低頻度語数:', len(words_unk)) # words_unkはunkに変換された単語のリスト
words = sorted(list(set(words)))
print('total words:', len(words))
word_indices = dict((w, i) for i, w in enumerate(words)) # 単語をキーにインデックス検索
indices_word = dict((i, w) for i, w in enumerate(words)) # インデックスをキーに単語を検索
訓練データ作成
元データは文字列のリストなので、これを学習データにするには、先に作った辞書を使って数字に置き換える必要がある。置き換えの際に、低頻度単語には「UNK」文字列のインデックスを使用する。
入力の1文字に対し、出力は前後n文字の合計2n文字なので、入力次元は1、出力次元は2nである。ソース上では前後の文字数nを変数maxlenで指定している。
汎化性能獲得のため、一般にはコーパスを訓練データ/評価データ/テストデータの3つに分割するが、今回は未知データを予測の対象としないので、全データを訓練データに使用する。
maxlen = 10 # 前後の語数
mat_urtext = np.zeros((len(mat), 1), dtype=int)
for i in range(0, len(mat)):
# 出現頻度の低い単語のインデックスをunkのそれに置き換え
if mat[i] in word_indices :
mat_urtext[i, 0] = word_indices[mat[i]]
else:
mat_urtext[i, 0] = word_indices['UNK']
print(mat_urtext.shape)
len_seq = len(mat_urtext) - maxlen
data = []
target = []
for i in range(maxlen, len_seq):
data.append(mat_urtext[i])
target.extend(mat_urtext[i-maxlen:i])
target.extend(mat_urtext[i+1:i+1+maxlen])
x_train = np.array(data).reshape(len(data), 1)
t_train = np.array(target).reshape(len(data), maxlen*2)
z = zip(x_train, t_train)
nr.seed(12345)
nr.shuffle(z) # シャッフル
x_train, t_train = zip(*z)
x_train = np.array(x_train).reshape(len(data), 1)
t_train = np.array(t_train).reshape(len(data), maxlen*2)
print(x_train.shape, t_train.shape)
※Python 2対応。Python 3の場合は、
z = zip(x_train, t_train)の行を、
z = list(zip(x_train, t_train))に書き換える必要がある。
これを行わない場合、shuffle関数の行でTypeError: object of type 'zip' has no len()というエラーが発生する。
Copyright© Digital Advantage Corp. All Rights Reserved.