word2vecリターンズ! 品詞分類による精度改善:ディープラーニング習得、次の一歩(1/2 ページ)
Keras(+TensorFlow)を使って自然言語のベクトル化手法「word2vec」を実装。学習データに品詞分類を追加することによって、前回よりも予測精度が改善するかを検証する。
ご注意:本記事は、@IT/Deep Insider編集部(デジタルアドバンテージ社)が「deepinsider.jp」というサイトから、内容を改変することなく、そのまま「@IT」へと転載したものです。このため用字用語の統一ルールなどは@ITのそれとは一致しません。あらかじめご了承ください。
word2vecの意義と応用分野
word2vecとは文字どおり、単語(word)をn次元ベクトル(vector)に対応させること、つまり、各単語をn個の実数の組に対応させることであるが、重要なのはその表現に意味を持たせられることである。すなわち、word2vecの最大の特徴は、単語間の関係性をベクトル演算(足し引き)によって表現できるところである。属性の足し引きで別の単語を導出できる(例: king - man + woman = queen)ということは、よく考えてみると画期的なことである。
またword2vecは、単語の類似度も表現できる。このような特徴は、機械翻訳などに応用されているといわれている。派手な特徴のわりに、表に現れている機会は少ないような気がするが、簡単に面白い結果を得られるので、今後も研究と応用が進んでいく分野であると筆者は考えている。
本稿のゴール
本稿は前回に引き続いて、word2vecを取り上げる。今回は学習データに単語の品詞分類を追加することによって、ベクトル表現の精度を高める。前回同様、今回も江戸川乱歩の著作をコーパスに使用するが、「その登場人物の苗字と名前の組が、どれくらい当てられるようになるか」を評価する。
本稿では前回同様、Kerasを使って実装する。ただし、今回は複数種類の入出力(単語それ自体と、単語の品詞種別)を使用するので、これまでのSequentialモデルではなく、Functional APIを用いる。
なお、TensorFlowやKerasはインストール済みを前提に論を進める。
前回のおさらい
前回は、江戸川乱歩の著作に京大黒橋・河原研究室のJUMAN++を適用して品詞分解し、これをコーパスとしてword2vecを実際に試してみた。JUMAN++については以下のURLを参照されたい。
今回も全く同じデータを使用する。具体的には、青空文庫から江戸川乱歩の著作を入手して使用した。JUMAN++を使って、対象文章から、分かち書きされた出力をカンマ区切りで得て、これをCSVファイルとして保存しておく。
word2vecには、
- CBOW(Continuous Bag-of-Words Model)
- Continuous Skip-gram Model(以下、skip-gramと表記)
の2つの手法があるが、これらのうちskip-gramを採用してニューラルネットワークを構築した。skip-gramは特定の単語が与えられたときに、その前後の複数の単語を当てようというものである。
ニューラルネットワーク構築に当たっては、Kerasを使用した。EmbeddingとDenseのわずか2層で構築できる。学習後のEmbedding層の重み行列が、求めるベクトル表現である。
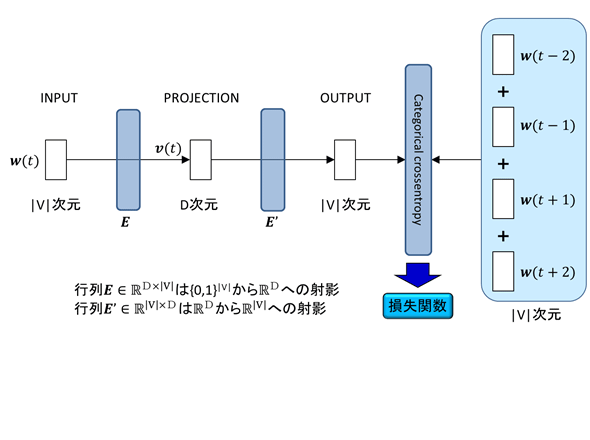
予測単語すなわちラベルデータが複数あるので、各ラベルデータに対応するone-hotベクトル(1つの次元だけが1で他が0のベクトル)を事前に足しあわせて「n-hotベクトル」的なラベルに整形し、これを使って訓練を実施した。図1にイメージを示す。
図においてVは語彙集合、|V|はその要素数すなわち語彙数、Dは埋め込みベクトルの次元である。また、wは各単語のone-hotベクトル表現、vはその埋め込みベクトル表現、Eはwからvへの変換行列、E'はvを|V|次元空間に射影する行列である。
品詞分類データの入手
JUMAN++の形態素解析結果には、品詞情報が含まれている。CSVファイルの4列目以降にそれが現れるが、このうち4列目と6列目を組み合わせて、品詞分類を実施する。
……省略……
蕗屋,蕗屋,蕗屋,名詞,6,普通名詞,1,*,0,*,0,自動獲得:Wikipedia Wikipediaページ内一覧:江戸川乱歩の美女シリーズ 読み不明
清一郎,せいいちろう,清一郎,名詞,6,人名,5,*,0,*,0,人名:日本:名:1686:0.00011
……省略……
この例なら「名詞_普通名詞」「名詞_人名」というように品詞分類を行う。
各単語に対応する品詞分類のリストを作成し、そこから訓練データや、インデックス←→品詞分類の辞書を作成したりする。後述のコード(リスト4)参照。
正解率算出の見直し
前回はcompileメソッドがデフォルトで出力する正解率をそのまま評価に使っていたが、よく考えてみると、ラベルデータがone-hotベクトルではないので、正解率の算出方法を別途考案する必要がある。
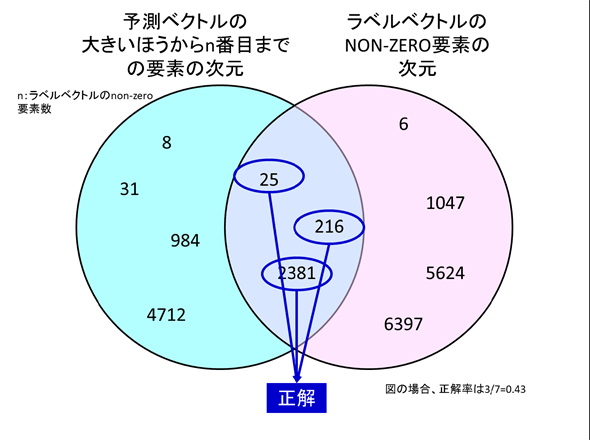
そこで、ラベルベクトルのnon-zero要素数をn個とするとき、予測ベクトルの大きい方からn個の各データの次元のうち、ラベルベクトルのnon-zero要素の次元と一致したものの数が正解数、これをnで割った値が正解率である、と定義することにした。文章では分かりにくいので、以下の図を参照してイメージをつかんでいただきたい。
Kerasには、自作した評価関数を登録する機能があるが、上記の処理を評価関数として実装することは筆者の手に余ったので(爆)、訓練後に評価することにした。コードは後述する。訓練の進行に伴って、ここで算出した正解率が改善するかどうか、気になるところであるが、これは確かに改善することを確認した。
埋め込みベクトル次元の拡大
いよいよ、品詞分類を適用したword2vecに取りかかるが、その前に、埋め込みベクトル次元数を大きくして、予測精度がどの程度改善するか見てみることにする。
前回の記事では、埋め込みベクトル次元数を100としていたが、これを400にしてみる。評価尺度は、正解率の他に、作品中の登場人物の苗字と名前の組み合わせを当てられるかどうかで判断する。
評価に使用する登場人物の氏名は以下のとおりである。
| 苗字 | 名前 | 登場作品 |
|---|---|---|
| 黒田 | 清太郎 | 一枚の切符 |
| 蕗屋 | 清一郎 | 心理試験 |
| 斎藤 | 勇 | 心理試験 |
| 松村 | 武 | 二銭銅貨 |
| 人見 | 廣介 | パノラマ島綺譚 |
| 菰田 | 源三郎 | パノラマ島綺譚 |
| 郷田 | 三郎 | 屋根裏の散歩者 |
| 岩瀬 | 早苗 | 黒蜥蜴 |
| 雨宮 | 潤一 | 黒蜥蜴 |
| 桜山 | 葉子 | 黒蜥蜴 |
| 岩瀬 | 庄兵衛 | 黒蜥蜴 |
| 表1 登場人物氏名一覧 | ||
これらに対し、埋め込みベクトル表現演算、
「明智」 − 「小五郎」 + 予測対象の名前
の結果が「予測対象の名字」であれば正解であるとする。例えば「明智 − 小五郎 + 清太郎」の結果が「黒田」であれば正解である。
前回記事のリスト5の「vec_dim」の値を、100から400に変えて実行する。以下がその結果である。
| 埋め込み次元 | 100 | 400 |
|---|---|---|
| 正解率 | 0.389271 | 0.393821 |
| 黒田清太郎 | × | × |
| 蕗屋清一郎 | × | × |
| 斎藤勇 | × | × |
| 松村武 | × | × |
| 人見廣介 | × | ○ |
| 菰田源三郎 | × | ○ |
| 郷田三郎 | × | ○ |
| 岩瀬早苗 | × | × |
| 雨宮潤一 | × | × |
| 桜山葉子 | × | × |
| 岩瀬庄兵衛 | × | ○ |
| 表2 次元数を変化させた時の正解率の変化 | ||
正解率はほとんど変わらないが、苗字当ては劇的に改善した。以降、埋め込み次元数=400で評価を進めることにする。
品詞分類を適用したword2vecの実装
参考情報として、筆者が実行したソースコードを以下に示す。これらをJupyter Notebook上で、コードブロック単位に実行した。使用した各種ソフトのバージョンは、以下のとおりである。
- Python: 3.6.4
- Anaconda: 5.1.0
- TensorFlow(with GPU): 1.3.0
- Keras: 2.1.4
- Jupyter Notebook: 4.4.0
まず、各種import宣言である。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import csv
import pandas as pd
import random
import numpy.random as nr
import sys
import h5py
import keras
import math
from __future__ import print_function
from keras.layers.core import Activation
from keras.layers.core import Dense
from keras.layers.core import Flatten
from keras.layers.embeddings import Embedding
from keras.models import Sequential
from keras.layers import Input
from keras.models import Model
from keras.callbacks import EarlyStopping
from keras.initializers import glorot_uniform
from keras.initializers import uniform
from keras.optimizers import RMSprop
from keras.utils import np_utils
次に、CSV読み込み処理であるが、これは前回記事と同じである。
# 元データ
df1 = csv.reader(open('rampo_separate.csv', 'r'))
df2 = csv.reader(open('rampo_separate2.csv', 'r'))
df3 = csv.reader(open('rampo_separate3.csv', 'r'))
data1 = [ v for v in df1]
data2 = [ v for v in df2]
data3 = [ v for v in df3]
mat1 = np.array(data1)
mat2 = np.array(data2)
mat3 = np.array(data3)
mat = np.r_[mat1[:,0],mat2[:,0],mat3[:,0]]
print(mat.shape)
品詞データ作成処理
CSVファイルの4列目と6列目の情報を_でつないで、1つの品詞情報に整形している。これから、品詞情報用辞書や学習データを作成する。
mat_part_of_speech1 = np.r_[mat1[:,3],mat2[:,3],mat3[:,3]] # 品詞
mat_part_of_speech2 = np.r_[mat1[:,5],mat2[:,5],mat3[:,5]] # 品詞詳細
mat_part_of_speech = []
for i in range (0,len(mat_part_of_speech1)) :
mat_part_of_speech.append( mat_part_of_speech1[i] +'_'+ mat_part_of_speech2[i])
# サンプルとして1つ出力
print(mat[10])
print(mat_part_of_speech[10])
辞書データの作成
出現する単語に一意のインデックス番号を付与し、インデックス←→単語文字列の両引きが出来る辞書を作成する。これも、前回記事とほとんど同じである。
words = sorted(list(set(mat)))
cnt = np.zeros(len(words))
print('total words:', len(words))
word_indices = dict((w, i) for i, w in enumerate(words)) # 単語をキーにインデックス検索
indices_word = dict((i, w) for i, w in enumerate(words)) # インデックスをキーに単語を検索
# 単語の出現数をカウント
for j in range (0, len(mat)):
cnt[word_indices[mat[j]]] += 1
# 出現頻度の少ない単語を「UNK」で置き換え
words_unk = [] # 未知語一覧
for k in range(0, len(words)):
if cnt[k] <= 3 :
words_unk.append(words[k])
words[k] = 'UNK'
print('UNK words:', len(words_unk)) # words_unkはunkに変換された単語のリスト
words = sorted(list(set(words)))
print('total words:', len(words))
word_indices = dict((w, i) for i, w in enumerate(words)) # 単語をキーにインデックス検索
indices_word = dict((i, w) for i, w in enumerate(words)) # インデックスをキーに単語を検索
品詞データ用辞書作成
単語用の辞書と同じ要領で、品詞情報にインデックスを振り、辞書を作成する。
parts = sorted(list(set(mat_part_of_speech)))
print('total parts:', len(parts))
parts_indices = dict((w, i) for i, w in enumerate(parts)) # 単語をキーにインデックス検索
indices_parts = dict((i, w) for i, w in enumerate(parts)) # インデックスをキーに単語を検索
訓練データ作成
単語用の訓練データに加えて、品詞用の訓練データも同時に作成する。ロジックはどちらも同じで、元データの文字列を、先に作った辞書を使って数字に置き換える。
maxlen = 10 # ウィンドウサイズ
mat_urtext = np.zeros((len(mat), 1), dtype='int16')
for i in range(0, len(mat)):
# 出現頻度の低い単語のインデックスをunkのそれに置き換え
if mat[i] in word_indices :
mat_urtext[i,0]=word_indices[mat[i]]
else:
mat_urtext[i,0]=word_indices['UNK']
mat_parts = np.zeros((len(mat_part_of_speech),1), dtype='int8')
for i in range(0,len(mat_part_of_speech)):
mat_parts[i,0] = parts_indices[mat_part_of_speech[i]]
len_seq = len(mat_urtext) - maxlen
x_train = np.zeros((len_seq-maxlen,1), dtype='int16')
t_train = np.zeros((len_seq-maxlen,maxlen*2), dtype='int16')
x_p_train = np.zeros((len_seq-maxlen,1), dtype='int8')
t_p_train = np.zeros((len_seq-maxlen,maxlen*2), dtype='int8')
for i in range(maxlen, len_seq):
# 単語
x_train[i-maxlen,0] = mat_urtext[i]
t_train[i-maxlen,0:maxlen] = np.array(mat_urtext[i-maxlen:i]).reshape(1, maxlen)
t_train[i-maxlen,maxlen:maxlen*2] = np.array(mat_urtext[i+1:i+1+maxlen]).reshape(1, maxlen)
# 品詞
x_p_train[i-maxlen,0] = mat_parts[i]
t_p_train[i-maxlen,0:maxlen] = np.array(mat_parts[i-maxlen:i]).reshape(1, maxlen)
t_p_train[i-maxlen,maxlen:maxlen*2] = np.array(mat_parts[i+1:i+1+maxlen]).reshape(1, maxlen)
z = list(zip(x_train,t_train,x_p_train,t_p_train))
nr.seed(12345)
nr.shuffle(z) # シャッフル
x_train,t_train,x_p_train,t_p_train = zip(*z)
x_train = np.array(x_train).reshape(len_seq-maxlen,1)
t_train = np.array(t_train).reshape(len_seq-maxlen, maxlen*2)
x_p_train = np.array(x_p_train).reshape(len_seq-maxlen, 1)
t_p_train = np.array(t_p_train).reshape(len_seq-maxlen, maxlen*2)
print(x_train.shape, t_train.shape, x_p_train.shape, t_p_train.shape)
Copyright© Digital Advantage Corp. All Rights Reserved.